Algorithmic tools from optimization have had become more and more important in machine learning and data analysis over the past 15 years. For much of this time, the focus has been on tools from convex optimization. The best known problems in data analysis (such as kernel learning, linear regression and classification, and logistic regression) gave rise to convex problems, for which algorithms are guaranteed to find the global solution, often with theoretical bounds on the runtime required to find the solution in terms of the number of data features, the size of the data set, and the precision required.
Increasingly, the focus is shifting to nonconvex optimization, in which the functions to be minimized may have a plethora of local solutions and saddle points. (The latter are points where the function is flat, yet there are some directions leading away from the point in which the function increases and others in which it decreases.) Nonconvex problems appear in the hottest area of machine learning – deep learning – as well as in matrix and tensor completion problems and in robust statistics. Some algorithms from convex optimization can be adapted to nonconvex optimization, at the expense of substantial complication and the loss of complexity guarantees. Several proposals made during the past two years have been remarkably complicated.
IFDS researchers have been working on algorithms for nonconvex optimization problems that can potentially be applied in these settings. Our goals are to define methods that are significantly less complicated than those that have been proposed to date, and are close to methods that would be applied in practice, yet match the best known complexity bounds. In a recent paper, IFDS researchers Clement Royer and Stephen Wright have proposed a method that uses search directions of several different types (including gradient descent directions, Newton directions, and negative curvature directions) in conjunction with a standard backtracking line search technique. They prove that indeed it achieves the best known complexity, using an algorithm design and analytical techniques that are more elementary than those proposed earlier. Royer and Wright are currently extending the method to address larger classes of nonconvex optimization problems, while designing careful implementations that can be used to solve practical problems in data science.
Royer and Wright’s paper can be found on the arXiv at https://arxiv.org/abs/1706.03131
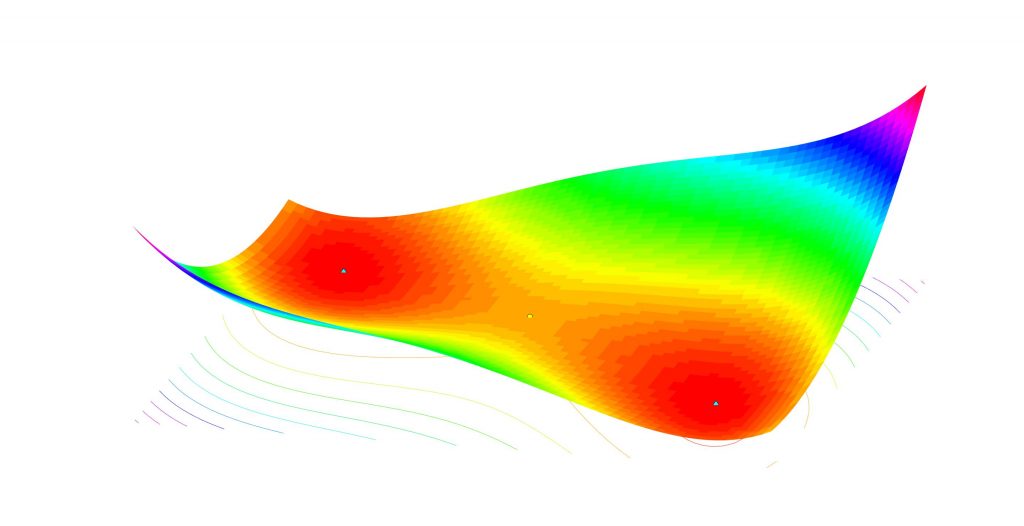
[The figure shows a nonconvex function with two local minima (blue diamonds) and one saddle point (yellow dot). The algorithm we describe will converge to one of the local minima, depending on its starting point.]